Scalable automated parallel PDE-constrained optimisation for dolfin-adjoint
eCSE02-03Key Personnel
PI/Co-I: Patrick E. Farrell - University of Oxford; Michele Weiland - EPCC
Technical: Dominic Sloan-Murphy - EPCC
Relevant documents
eCSE Final Report: Scalable automated parallel PDE-constrained optimisation for dolfin-adjoint
Project summary
The dolfin-adjoint package enables the automated optimisation of problems constrained by partial differential equations (PDEs). These problems are ubiquitous in engineering with examples including the design of wings to maximise lift, identification of the optimal placement of marine turbines for renewable tidal energy, the design of the cheapest bridge that will support its load, and the imaging of underground structures for petroleum exploration.
Prior to this project, dolfin-adjoint was limited to serial optimisation libraries with no concept of parallel linear algebra. Data was therefore required to be shared with all ranks and optimisation calculations performed redundantly. Now, the software is equipped with a Python-based interface to the parallel algorithms included in PETSc (the "Portable, Extensible Toolkit for Scientific Computation"), thereby eliminating the performance penalty associated with gathering the data and lifting the upper bound on the size of problems able to be considered.
The algorithms within the PETSc TAO (Toolkit for Advance Optimization) module were themselves extended to improve the efficiency of their solves. Specifically, the ability for a user to provide a Riesz map for the important LMVM, BLMVM, NTR, and NLS [1] solvers was added, allowing for use of a more appropriate inner product for a problem and enabling mesh-independent convergence, i.e. the number of iterations no longer depends on the complexity of the mesh.
This addition has had a dramatic effect on the performance of said solvers. Results for the Poisson mother problem [2] with a given mesh at various levels of random refinement, are provided in Table 1-1 below.
As an illustrative example of the improvement in efficiency, Figure 1-1 and Figure 1-2 give a visualisation of the convergence for the Poisson mother problem after 40 BLMVM iterations on a given mesh without the Riesz map specified, and after 3 iterations with the map correctly set.
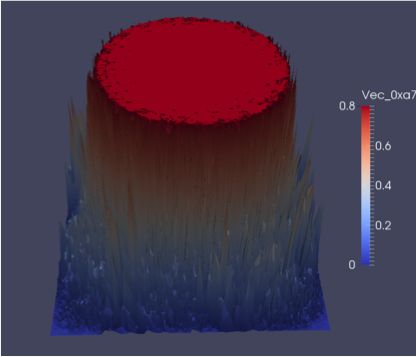
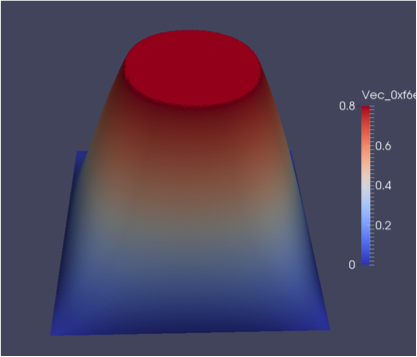
To the best of our knowledge, no other open-source package has managed to attain mesh independence in the bounded case (BLMVM), making this a significant achievement.
Additionally, this project investigated the checkpointing I/O performance of dolfin-adjoint, necessary during simulations with long time horizons on platforms with limited memory.
The previous implementation gathered all data to a single root process which would write out in XML format. This was replaced with a scalable HDF5-based solution built on work from a previous dCSE project involving the implementation of parallel I/O for the FEniCS software package [3].
Looking at a sensitivity analysis of the heat equation on a Gray's Klein bottle, the results in Figure 1-3 were observed on ARCHER.
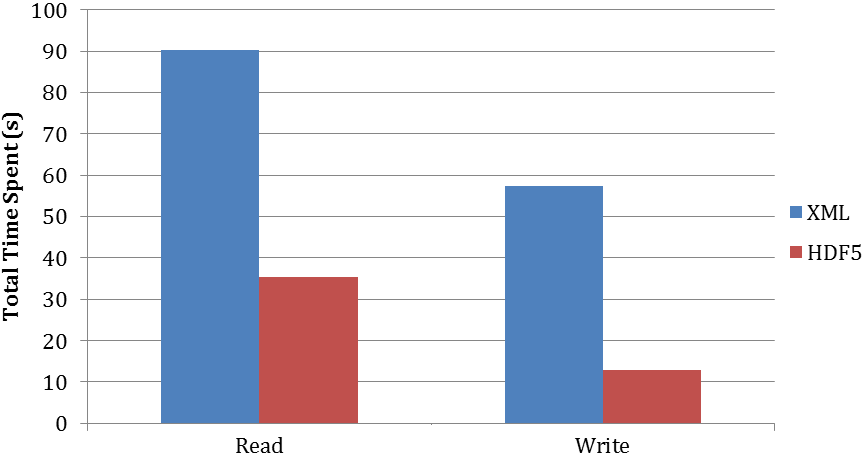
In this case, read times attain a speed up factor of approximately 3 with the new HDF5 approach while writes reach close to 5 times faster. This opens the door to solving problems which have been bottlenecked by the limited I/O bandwidth of a single process or by the overheads of having to communicate all data to that single rank.
Summary of the software
All software outputs from the project have been merged into the master branches of the associated software, located at:
- dolfin-adjoint (Primary)
https://bitbucket.org/dolfin-adjoint/dolfin-adjoint - PETSc
https://bitbucket.org/petsc/petsc - petsc4py Fork
https://bitbucket.org/petsc/petsc4py
A pull request was made to have changes merged into the main PETSc and petsc4py codebases. The work of the project has been accepted into the main "master" branch of all codes involved.
The new functionality will be incorporated into a future PETSc release and made available to the entire user community.
On ARCHER, PETSc is fully supported and maintained by Cray. It is expected that the version containing the output of this project will be installed as part of the regular update cycle of the Cray XE/XK Programming Environment. The enhanced petsc4py and dolfin-adjoint dependent on this release will subsequently be installed as central ARCHER packages.
Prior to this, ARCHER users will be able to access the software via the public repositories and employ the system development tools to install a local version for their own use.
Links and References:
[1]: TAO 3.6 Users Manual, Retrieved 18 August 2015, from:
http://www.mcs.anl.gov/petsc/petsc-current/docs/tao_manual.pdf
[2]: Optimal control of the Poisson equation, Retrieved 18 August 2015,
from:
http://www.dolfin-adjoint.org/en/latest/documentation/poisson-mother/poisson-mother.html
[3]: University Distributed CSE Project Report Expressive and scalable
finite element simulation beyond 1000 cores, Retrieved 18 August 2015,
from:
http://www.hector.ac.uk/cse/distributedcse/reports/UniDOLFIN/UniDOLFIN/dcse_richardson_wells.html
Project Website:
http://www.dolfin-adjoint.org/en/latest/






