Performance enhancement in R-matrix with time-dependence (RMT) codes in preparation for application to circular polarised light fields

Key Personnel

PI/Co-I: Prof Hugo van der Hart - Queen's University Belfast; Dr Martin Plummer - STFC

Technical: Dr Jonathan Parker - Queen's University Belfast

Relevant Documents

eCSE Technical Report: Performance enhancement in R-matrix with time-dependence (RMT) codes in preparation for application to circular polarised light fields

Project summary

The RMT method is a new method for solving the time-dependent Schroedinger Equation, the fundamental equation of motion for objects at the atomic and sub-atomic level. RMT solves the Schroedinger Equation for many-electron atoms (and molecular systems) driven by intense short laser pulses. Although several other time-dependent R-Matrix methods have been introduced in recent years, the RMT approach demonstrates great efficiency and accuracy, primarily because it employs finite-difference (FD) techniques to model the ejected electron far from the atomic core. The difficult problem of merging an R-Matrix basis set model (near to the atomic core) with a spatially adjacent FD model (far from the atomic core) while maintaining the correctness of the solutions has been a long-standing barrier to progress in this field, but we have recently shown that this method is capable of maintaining correctness to 1 part in 10¹².

In the last year we have started to apply the codes to increasingly difficult problems, for example studies of the influence of atomic structure on the ionization of Ne⁺ in intense laser radiation. These calculations are two orders of magnitude more computationally demanding than problems we worked on previously. To maintain good efficiency in the numerical algorithms, we needed to redesign the RMT communications packages used to parallelise the code, and also redesign the algorithm that allocates CPU cores to the various computations that RMT performs.

In the first phase of the project a new algorithm was developed for assigning CPU cores to the matrix-vector multiplications that form the bulk of the computation performed by RMT. The new algorithm produced a factor of 5 speed-up of the numerical integration, which turns out to be an essential optimization in the new class of physical problems this project was designed to address.

The improvements in efficiency are shown in the figure below. The example problem is an integration of the Ne⁺ atom in ultraviolet laser radiation. Ne⁺ is modeled using 23 symmetries, each of which includes several matrix-vector multiplications. In this example, RMT uses one to 15 CPU cores per symmetry to perform these matrix-vector multiplications. Each symmetry communicates with neighboring symmetries, which ultimately hampers parallelization. Since the different symmetries use different lengths of basis expansion, the problem is to find the right distribution of CPU cores over the symmetries to maximise performance, and to rewrite the code to perform the new allocation automatically.

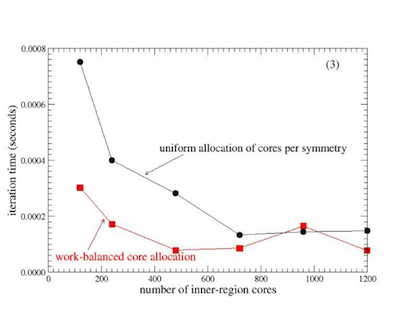
The figure shows the speed-up obtained by the new strategy (red line). A factor of 5 improvement is observed when 56 cores are used by the inner region integration. Beyond 56 cores little improvement is obtained (red line), because communications overhead dominates. The old strategy (black line) shows gradual improvement as more cores are added, but even the use of 138 cores produces an executable that runs at half the speed of the new version with 56 cores.

In phases 2 and 3, we examined the initial set-up of the calculations. The original RMT code would input potentially large data files upon initialisation, and store them on a single CPU core, effectively limiting the size of the data files to a few gigabytes at most. The redesigned code reduces this storage requirement (per CPU core) to a small fraction of the original size, usually by inputting the files incrementally. In phase 3, the objective was achieved by parallelising the input so that each core reads a small amount of data independently of the others. The optimisations outlined here taken together will make it possible to treat a class of atom-laser interactions in which the fields are elliptically polarized, a problem which effectively raises the dimension of the partial differential equation being solved by RMT, and will likely require the processing power of the next generation of supercomputers.

Achievement of objectives

This project largely involved the optimisation of the inner-region communication algorithms of the RMT code. The new communications design enabled a new load balancing algorithm, which increased the speed of the code by up to a factor of 5, and reduced the amount of RAM used during initialisation by one or more orders of magnitude.

The project was organized in 3 phases. In Phase 1 a new load balancing procedure was developed for assigning cores to the computationally demanding inner region matrix-vector multiplications, which dominate the calculation in the inner-region. Phases 2 and 3 of the project were a redesign of the initialization process for the largest data structures used by the inner region R-Matrix integration. In Phase 2 the objective of the redesign was to reduce memory use during input of the data files containing dipole matrix elements between different symmetries and wavefunction files, describing the wavefunction associated with the ejected electron within the inner region. In Phase 3 a further redesign enabled full parallelisation of the input of the dipole potential matrix 'd' file and the wavefunction data file 'Splinewaves'.

All objectives were met in full. The new load balancing algorithm speeded up RMT runs by a factor of 5 in the test program. We predicted in the proposal that a factor of 6 would be possible. The factor of 6 can also be observed if special conditions are met, such as larger basis-set expansions, but the basic test routine demonstrates a factor of 5 for typical Fortran compilations on Archer. In Phase 2 objectives were met by reading each data file incrementally, distributing the data in small blocks, and repeating until end-of-file is reached. The original RMT code used a single MPI master task to read the full data file from the hard drive, and only then distribute portions of it to other inner-region cores. The new approach allows the RMT code to tackle problems with data structures that are up to two orders of magnitude larger, allowing us to tackle a class of problems that were considered intractable a few years ago.

Finally, the objectives of Phase 3 were met by fully parallelising input of the field-free Hamiltonian 'd', the largest data structure used by RMT. In the original design, the 'd' file was read in its entirety by a single MPI task, processed, and distributed to each of the inner region cores. Now each of the inner region cores reads a small portion of 'd', and does so independently of every other core, and in parallel.

Summary of the software

The R-matrix with time dependence (RMT) code is a specialised world-leading code for the time-dependent description of multi-electron systems embedded in intense light fields. It has been developed at Queen's University Belfast over the last 6 years as part of the EPSRC-funded UK-RAMP project. Over the last three years, it has demonstrated a world-leading capability for the description of single-ionization processes in multi-electron atoms irradiated by intense laser light.

As part of the UK-RAMP project, the code is available to the UK community through collaboration with the QUB development team. Efficient use of the code will require detailed understanding of the code, and detailed understanding of the parallelisation and the implementation of parallelism within the code. In addition, the accuracy of the calculations is critically dependent on the appropriate setting of the input parameters. Hence, through collaboration with QUB, new users will obtain the required training to make best use of the codes. The RMT codes require the use of B-spline basis sets in the generation of R-matrix input data. It is intended that the R-matrix code using B-spline basis sets developed for this purpose will be made available to the community shortly as part of the latest R-matrix code developments. The development of a molecular RMT code will also be assisted by the developments in this project. The molecular RMT code will be based on the atomic codes, and the new routines should therefore slot into the molecular codes as well.